Selection sort:
总体结构:两层for loop。
外层:从index i = 0到index i = N遍历整个Comparable[] a。
内层:
- 初始给min(最小值的index)赋值为i
- 从i到N遍历,如果有比最小值更小的值(j),赋值min = j
- 内层遍历结束后,交换最小值和i的位置。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public static Selection {
public static void sort(Comparable[] a) {
int N = a.length;
for (int i = 0; i < N; i++) {
int min = i;
for (int j = i + i; j < N; j++) {
if (less(a[j], a[min])) {
min = j
}
exchange(a, i, min);
}
}
}
public static boolean less(Comparable v, comparable w) {
return v.compareTo(w) < 0;
}
public static void exchange(Comparable[] a, int i, int j) {
Comparable swap = a[i];
a[i] = a[j];
a[j] = swap;
}
}
Mathematical analysis:

Insertion Sort
总体结构:两层for loop
外层:从index i=0到index i=N遍历整个Comparable[] a。
内层:j = i, 从 j 往回到 0 遍历,如果 a[j - 1] 大于 a[j] ,则交换a[j-1]和a[j]的位置;如果a[j-1] 小于等于a[j],跳出遍历。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public class Insertion {
public static void sort(Comparable[] a) {
int N = a.length;
for (int i = 0; i < N; i++) {
for (int j = i; j > 0; j--) {
if (less(a[j], a[j-1])) {
exchange(a, j, j-1);
} else {
break;
}
}
}
}
private static boolean less(Comparable v, Comparable w)
{ /* as before */ }
private static void exchange(Comparable[] a, int i, int j)
{ /* as before */ }
}
Mathematical analysis:
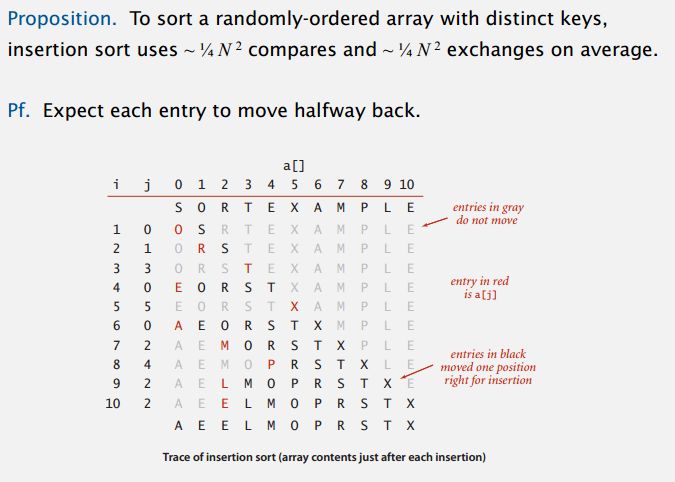
Worst case:
- compares = (N-1)+(N-2)+(N-3)+…+2+1=((N-1)+1)*(N-1)/2=N^2/2-N/2;
- exchanges = (N-1)+(N-2)+(N-3)+…+2+1=((N-1)+1)*(N-1)/2=N^2/2-N/2;
- total operations = N^2-N;
- time complexity: O(N^2).
Best case: If the array is in ascending order, insertion sort makes N-1 compares and 0 exchanges.
特别地,对于partially-sorted array, 利用insertion sort来排序只需要constant time。
- Definition of inversion: a pair of keys that are out of order, 也就是一对需要交换位置的元素。
- Def: An array is partially sorted if the number of inversions is ≤ c N, 也就是说当需要交换位置的元素对于整个array来说是constant,需要交换位置的元素相对整个array来说很小,才满足partially sorted array.
- 举例:A sub-array of size 10 appended to a sorted sub-array of size N.
- 举例:An array of size N with only 10 entries out of place.
- Number of exchanges equals the number of inversions.
Shellsort
属于insertion sort的升级法,原理是把一次走一步变成一次走h步,called h-sorted array。相比insertion sort更加有效率。
总体结构:两层for loop。
外层:从index i = 步长h 开始,到 index i = N,遍历Comparable[] a.
内层:从index j = i开始,
- 如果 j 大于步长h 且 a[j] < a[j-h]; j-=h { 交换a[j] 和 a[j-h] 的位置}
- else {跳出内层for loop}.
特点:A g-sorted array remains g-sorted after h-sorting it.
Great increment sequence to use: 3*x+1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public class Shell {
public static void sort(Comparable[] a) {
int N = a.length;
int h = 1;
while (h < N/3) h = 3 * h + 1; // 1, 4, 13, 40, 121, 364, ...
while (h >= 1) {
for (int i = h; i < N; i++) {
for (int j = i; j >= h && less(a[j], a[j-h]); j -= h) {
exchange(a, j, j-h);
}
h = h/3;
}
}
}
private static boolean less(Comparable v, Comparable w)
{ /* as before */ }
private static void exchange(Comparable[] a, int i, int j)
{ /* as before */ }
}
