一、树的旋转

先从树旋转说起：
p1
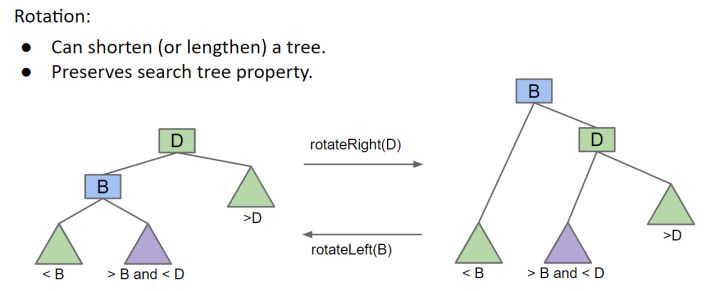
图左向图右的变化是以D为旋转点的右转(rotateRight(D))，旋转点D的左子B移动到顶端，D旋转到右下成为B的右子，同时B的右子(>B and <D)连接到D，成为D的左子。右转会缩短tree左侧的高度，增加tree右侧的高度。

图右往图左的变化是以B为旋转点的左转(rotateLeft(B)), 旋转点B的右子D移动到顶端，B旋转到左下成为D的左子，同时D的左子(>B and <D)链接到B，成为B的右子。左转会增加tree左侧的高度，缩短tree右侧的高度。

二、红黑树

红黑树(这里只说Left-leaning)利用Binary Search Tree(BST)结构，对2-3树进行实现。

2-3树与原始BST的区别是（2个需要解决的问题）：

  1. BST结构里，每个node只有1个key value和左右两分支，而2-3树的单个node既可以有1个key-value和左右两分支(2-nodes)；也可以有2个key-value和左中右三分支(3-nodes)。
  2. BST结构不需要平衡，而2-3树必须平衡（所有leaf到root的距离相等）。

问：如何解决第一个问题，从而实现3-nodes的情况？
p2
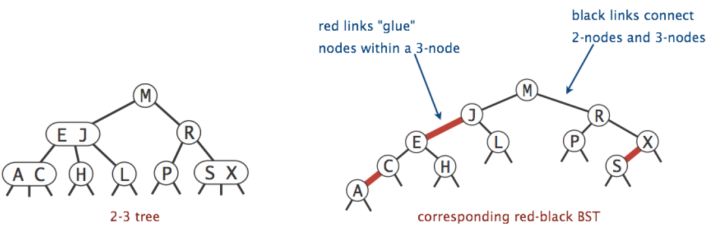
左倾红黑树用红色的link表示2-3树中的3-nodes，3-nodes中较小的元素被下放到较大元素的左子node位置，二者用红色link连接。

问：如何在增删过程中保持树的平衡？

Insert操作
基本思想：将2-3树和左倾红黑树一一对应，根据2-3树的变化对红黑树进行操作。
原理：

  1. 添加：增加新元素时，根据原始BST的查找原理，找到合适位置后，默认给新增node添加红色link（也就是与找到的node并列）。此时可能会出现4-node，但没有关系我们会进行处理。
  2. 处理：由recursion原理，插入处为recursion最底层。从底层到最顶层的root，每层都检查是否需要做旋转或翻转变换。
    • 出现右倾斜怎么办：左旋转
      p3
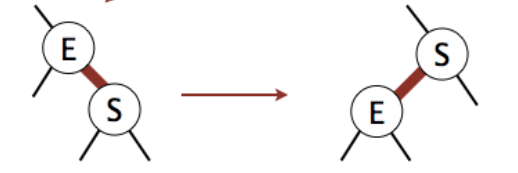
    • 出现连续的左倾斜怎么办：右旋转，再颜色翻转
      p4
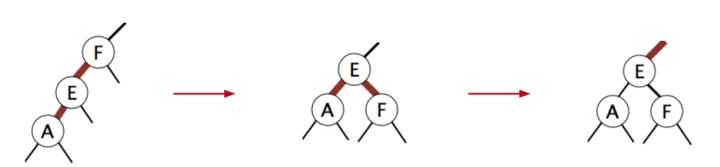
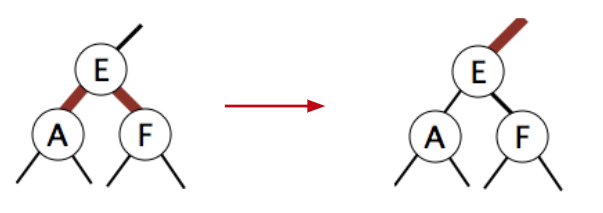
    • 出现三足鼎立怎么办：颜色翻转（翻转与E接触的所有link）
      p5
      Insert部分的代码：
      p6

复杂度：

  1. LLRB tree has height O(log N).
  2. Contain is trivially O(log N).
  3. Insert is O(log N).
    • O(log N) to add the new node.
    • O(log N) rotation and color flip operations per insert.