一、嵌套 for loop 的 runtime 不一定是 N²

Example：

public static void printParty(int N) {
    for (int i = 1; i <= N; i = i * 2) {
        for (int j = 0; j < i; j += 1) {
            System.out.println("hello");   
            int ZUG = 1 + 1;
        }
    }
}

这串代码的特点是，随着N从1开始递增，每到2的整数次方(N=1, 2, 4, 8, 16…)都是一个变动的节点，变动的值刚好为N。

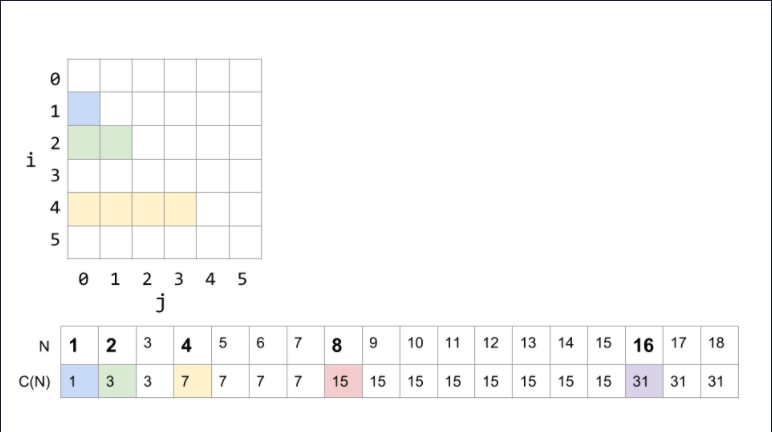
因此，在每个变动的阶段(if N is a power of 2), runtime = 2N-1.

如果我们在图中画出 [公式] 和 [公式] ，会发现这个嵌套for-loop的runtime被完全覆盖，因此该嵌套for-loop的runtime是线性的。

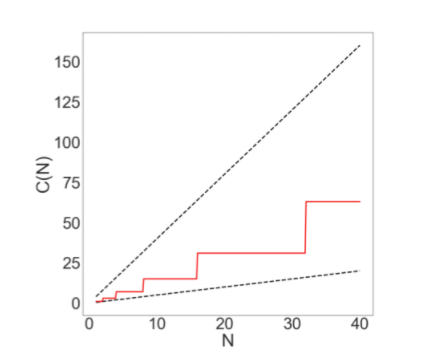
二、Recursion 的 runtime

Example：

public static int f3(int n) {
    if (n <= 1)
        return 1;
    return f3(n-1) + f3(n-1);
}

这段代码，如果我们call f3(4), 会return两个 f3(3), 每个 f3(3) 又会return两个 f3(2)，每个 f3(2) 又会return两个 f3(1)，就像有丝分裂…… 最后return的值为 2^(N-1).

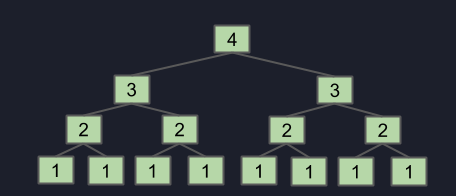
(f3(4) return的值为8)

直觉法：因为N每增加1，工作量是加之前的2倍，由此我们推测runtime为 2^(N)。

代数法：
C(1)=1; C(2)=1+2; C(3)=1+2+4;…; C(N)=1+2+4+…+2^(N-1). 由此算出 C(N)=2^(N) - 1.

递推法：
C(1)=1; C(2)=2C(1)+1; C(3)=2C(2)+1; …; C(N)=2*C(N-1)+1.
算出 C(N)=2^(N) - 1.

---

三、二分法的 runtime

二分法只对按顺序排列的list有效。原理是将最中间的元素与目标值对比，如果太大，排除大的那一半；如果太小，排除小的那一半。将剩下的一半不断重复取中值对比的过程，直到找到目标值。

最坏的结果：当目标值不在list中，从n个元素开始，变成n/2个元素，n/4个元素，直到剩下最后一个元素。每次都将list减半，所以在最坏的结果里，直觉上要重复 log2(n) 次 (不准确，因为在偶数个元素的list中，没有中间值，无法精准的减半)。

要精准的计算runtime, 我们需要计算具体减半的次数。

(runtime result)

从具体的数据可以看出，runtime只在N为2的次方时才增加， C(N)=⌊log2(N)⌋. (“⌊⌋”是floor function, 表示往下约等于最近的整数)。

几个性质：
⌊f(N)⌋ = Θ(f(N))
⌈f(N)⌉ = Θ(f(N))
log p(N) = Θ(log q(N))

最后这个说的是对于对数的runtime来说，底数是不重要的，因为依照Big O，它们都是等价的。因此 Θ(⌊log2(N)⌋)=Θ(logN)

(证明⌊f(N)⌋=Θ(f(N)))

很酷的事实：log time几乎和constant time 一样快，比linear time快，这就是为什么二分法很好用。

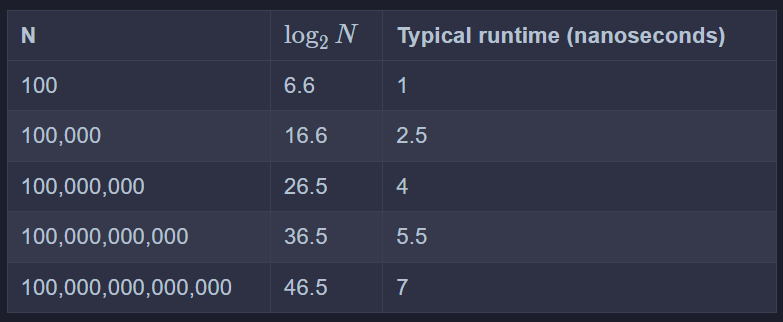(concrete log time)

四：合并排序（merge sort）的 runtime

目的：将两个sorted array合并为一个按顺序排列的array。

原理：对比两个sorted array的首位元素，将更小的那个放入目标array，重复这个步骤直到其中一个array为空，将另一个array剩余所有元素放进目标array。

runtime：目标array的长度N代表在最差的情况下，对比了N次，所以runtime为 Θ(N)。

五：合并排序（Merge sort）对 selection sort 的优化

复习一下selection sort：Elementary sorts

public static Selection {
    public static void sort(Comparable[] a) {
        int N = a.length;
        for (int i = 0; i < N; i++) {
            int min = i;
            for (int j = i + i; j < N; j++) {
                if (less(a[j], a[min])) {
                min = j
                }
            exchange(a, i, min);
            }
        }
    }
}

Selection sort 的runtime为 C(N)=N²/2 。用arbitrary units(AU)来表示，对N=64的list进行selection sort需要~2048 AU。 但假设我们把N=64的list分为两个N=32的list，单独进行selection sort，再进行merge sort，这样只需要512+512+64=1088 AU，相比前者快了很多。

假如我们再将两个N=32的list拆分成四个N=16的list，同样先单独进行selection sort，再进行merge sort，会更快吗？是的，1284+322+64=640.

假如对list不断拆分，直到每个list的length=1，就能直接进行merge sort了。

这就是merge sort的本质：

• If the list is size 1, return. Otherwise:
• Mergesort the left half
• Mergesort the right half
• Merge the results

Merge sort 的 running time： 将长度为 N 的list拆分到长度为 1 ，需要拆分 log2(N) 次。 对每层进行merge，runtime都是 N 。所以merge sort的runtime为 Θ(NlogN).

因此，相比runtime为 Θ(N²) 的selection sort，merge sort快很多。

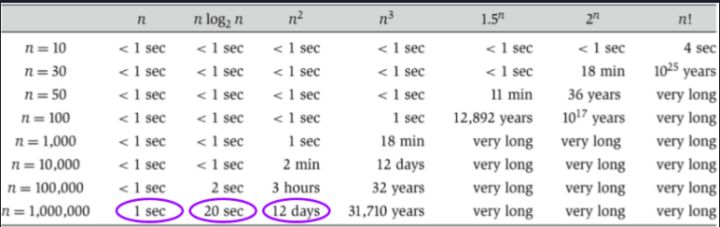
（不同runtime之间的对比）

---